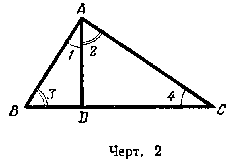МЕТРИЧЕСКИЕ  СООТНОШЕНИЯ    МЕЖДУ  ЭЛЕМЕНТАМИ
ПРЯМОУГОЛЬНОГО  ТРЕУГОЛЬНИКА.

2.(188.) Теорема. В прямоугольном треугольнике перпендикуляр, опущенный из вершины прямого угла на гипотенузу, есть средняя пропорциональная величина между отрезками, на которые основание перпендикуляра делит гипотенузу, а каждый катет есть средняя пропорциональная между гипотенузой и прилежащим к этому катету отрезком гипотенузы.

Пусть AD (черт. 2) есть перпендикуляр, опущенный из вершины прямого угла А на гипотенузу ВС. Требуется доказать следующие три пропорции:

1)  ^BD/_AD = ^AD/_DC ;      

2) ^BC/_AB =  ^AB/_BD ;      

3) ^BC/_AC = ^AC/_DC.      

Первую пропорцию мы докажем из подобия треугольников ABD и ADC. Эти треугольники подобны, потому что

/   1 = /   4 и    /  2 = /  3

как острые углы с соответственно перпендикулярными сторонами. Возьмём в /\  ABD те стороны BD и AD, которые составляют первое отношение доказываемой пропорции; сходственными сторонами в /\  ADC  будут AD и DC¹, поэтому

BD : AD = AD : DC.

_________________________________
 ¹Чтобы безошибочно определить, какие стороны взятых треугольников сходственны между собой, полезно держаться такого пути:
 1)  указать углы, против которых лежат взятые стороны одного треугольника;
 2)  найти равные им углы в другом треугольнике;
 3)   взять противолежащие им стороны.
   Например, для треугольников ABD и ADC рассуждаем так: в. треугольнике ABD стороны BD и AD лежат против углов 1 и 3; в треугольнике ADC этим углам равны 4 и 2; против них лежат стороны AD и DC. Значит, стороны AD и DC сходственны со сторонами BD и AD.

Вторую пропорцию докажем из подобия треугольников ABC и ABD. Эти треугольники подобны, потому что они прямоугольные и острый угол В у них общий. В /\  ABC возьмём те стороны ВС и АВ, которые составляют первое отношение доказываемой пропорции; сходственными сторонами в /\  ABD будут АВ и BD; поэтому

ВС : АВ = АВ : BD.

Третью пропорцию докажем из подобия треугольников ABC и ADC. Эти треугольники подобны, потому что они оба прямоугольные и имеют общий острый угол С.
В /\  АВС возьмём стороны ВС и АС; сходственными сторонами в /\  ADC будут АС и DC; поэтому

ВС : АС = AC: DC.

3. (189.) Следствие. Пусть А (черт. 3) есть произвольная точка окружности, описанной на диаметре ВС.

Соединив концы диаметра с этой точкой, мы получим прямоугольный /\  ABC, у которого гипотенуза есть диаметр, а катеты суть хорды (по свойству вписанного угла, опирающегося на диаметр). Применяя доказанную выше теорему к этому треугольнику, приходим к следующему заключению:

Перпендикуляр, опущенный из какой-либо точки окружности на диаметр, есть средняя пропорциональная величина между отрезками, на которые основание перпендикуляра делит диаметр, а хорда, соединяющая эту точку с концом диаметра, есть средняя пропорциональная между диаметром и прилежащим к хорде отрезком диаметра.

4. (190.) Задача. Построить отрезок, средний пропорциональный между двумя отрезками а и b.

Задачу эту можно решить двояким путём:

1) На произвольной прямой (черт. 4) откладываем отрезки АВ = а и ВС = b; на АС, как на диаметре, описываем полуокружность; из В восставляем до пересечения с окружностью перпендикуляр BD. Этот перпендикуляр и есть искомая средняя пропорциональная между АВ и ВС.

2)  На произвольной прямой (черт. 5) откладываем от точки А отрезки а и b. На большем из этих отрезков описываем полуокружность. Проведя из конца меньшего отрезка перпендикуляр к АВ до пересечения его с окружностью в точке D, соединяем А с D. Хорда AD есть средняя пропорциональная между а и b.

5. (191.) Теорема Пифагора. Доказанные выше теоремы позволяют обнаружить замечательное соотношение между сторонами любого прямоугольного треугольника. Это соотношение было впервые замечено греческим геометром Пифагором (VI в. до н. э.) и носит поэтому его имя — теорема   Пифагора.

Если стороны прямоугольного треугольника измерены одной и той же единицей, то квадрат длины  гипотенузы равен сумме квадратов длин катетов.

Пусть ABC (черт. 6) есть прямоугольный треугольник, AD — перпендикуляр, опущенный на гипотенузу из вершины прямого угла.

Положим, что стороны и отрезки гипотенузы измерены одной и той же единицей, причём получились числа а, b, с, с' и b' (принято длины сторон треугольника обозначать малыми буквами, соответствующими большим буквам, которыми обозначены противолежащие углы). Применяя теорему § 2 (188), можем написать пропорции:

а : с = с : с'   и  а : b = b : b',

откуда

ас' = с² и ab' = b².

Сложив  почленно  эти два  равенства,  найдём:

ас' + ab' = с² + b²,    или     а(с' + b') = с² + b².

Но с' + b' = а,  следовательно,

a² = с² + b².

Эту теорему обыкновенно выражают сокращённо так: квадрат гипотенузы равен сумме квадратов катетов.

Теорема Пифагора имеет ещё другую формулировку: площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на катетах.

Пример. Положим, что катеты, измеренные какой-нибудь линейной единицей, выражаются числами 3 и 4; тогда гипотенуза в той же единице выразится числом х, удовлетворяющим уравнению:

х²  = 3² + 4² = 9 + 16 = 25,     откуда        х = √25 = 5.

Замечание. Прямоугольный треугольник со сторонами 3, 4 и 5 называется часто египетским треугольником, так как он был известен ещё древним египтянам. Так, их землемеры для построения прямого угла на земной поверхности пользовались таким приёмов: бечёвку посредством узлов они разделяли на 12 равных частей; затем, связав концы, натягивали её на земле (посредством кольев) в виде треугольника со сторонами в 3, 4 и 5 делений; тогда угол между сторонами, равными 3 и 4, оказывался прямым¹.
_________________
 ¹ Прямоугольные треугольники, у которых стороны измеряются целыми числами, носят название пифагоровых треугольников. Можно доказать, что катеты х и у и гипотенуза z таких треугольников выражаются следующими формулами:

х = 2ab,       у = а² — b²,       z = а² + b² ,

где a и b — произвольные целые чцвяа при условии, что а > b.

6. (192.) Следствие. Квадраты катетов относятся между собой, как прилежащие отрезки гипотенузы. Действительно, из уравнений предыдущего параграфа находим:

c² : b² = ac' : ab' = с': b'.

7. (193.) Замечание.   К трём  равенствам, которые  мы  вывели выше:

1) ас' = с²;     2) ab' = b²   и    3) a² = с² + b²,

можно присоединить ещё следующие два:

4) b' + с' = а    и     5)  h² = b'с' '

(если буквой h обозначим длину высоты AD). Из этих равенств третье, как мы видели, составляет следствие первых двух и четвёртого, так что из пяти равенств только четыре независимы; вследствие этого можно по данным двум из шести чисел находить остальные четыре.

Для примера положим, что нам даны отрезки гипотенузы b' = 5 м и с' = 7 м; тогда

а = b' + с'  = 12;                             
с = √ac' = √12•7 = √84 = 9,165 ...
b = √ab' = √12•5 = √60 =  7,745 ...
 h = √b'c' = √5 • 7 = √35 =  5,916...  

МЕТРИЧЕСКИЕ  СООТНОШЕНИЯ    МЕЖДУ  ЭЛЕМЕНТАМИ
ПРЯМОУГОЛЬНОГО  ТРЕУГОЛЬНИКА.

§ 10. Числовая зависимость между линейными элементами
треугольников и некоторых четырёхугольников.

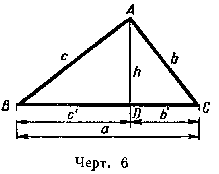
В прямоугольном треугольнике обозначают: а и b — катеты; с — гипотенуза;
а_с и b_с—проекции катетов а и b на гипотенузу; h — высота из вершины прямого угла. Предполагается, что отрезки измерены одной и той же единицей.

Пропорциональные отрезки в прямоугольном треугольнике.

1. Вычислить гипотенузу, если даны оба катета: 1) 12 см и 35 см; 2) 56 см и 33 см;
3) 4 м и 9 дм; 4) 60 см и 91 см;   5) 21 и 3¹/₄; 6)  ³/₂ и ⁷/₁₆;  7) 16,8 и 2,6; 8) 5 и 6.

2. Вычислить второй катет, если даны гипотенуза и первый катет:

1) 289 и 240; 2) 269 и 69; 3) 145 и 143; 4) 42,5 и 6,5; 5) 17 и 15²/₅; 6) 10 и 7.

В задаче 2 и во многих других случаях выгодно при вычислении разность квадратов заменять произведением суммы на разность

3. По двум данным элементам прямоугольного треугольника вычислить остальные четыре:

1) a = 15, b = 20;    2) a = 24, b = 7;    3) a = 4, b = 5;
4) a = 100, с = 125;    5) b = 65, с = 169;    6) а = 600, с = 625;
7) a = 6,  а_с = 3,6;      8) b = 7, b_с= 1,96;
9) с = 29, а_с= 15 ⁶/₂₉ ;    10) с = 3, b_с = 2;
11) а_с= l ¹/₂, b_с = 2 ²/₃;    12) а_с = 2, b_с= 18;
13) а = 136, h = 120;    14) b = 9, h = 8  ³²/₄₁? .

4. По данной сумме двух отрезков и среднему пропорциональному этих отрезков построить отрезки.

5. По данной разности двух отрезков и среднему пропорциональному этих отрезков построить отрезки.

6. Доказать, что в прямоугольном треугольнике ab = ch.

7. Катеты относятся, как 5:6, а гипотенуза равна 122 см. Найти отрезки гипотенузы, отсекаемые высотой.

8. Катеты относятся, как 3:2, а высота делит гипотенузу на отрезки, из которых один на 2 м больше другого. Определить гипотенузу.

9. Катеты относятся, как 3:7, а высота, проведённая на гипотенузу, равна 42 см. Определить отрезки гипотенузы.

10. Доказать, что диаметр окружности, вписанной в равнобедренную трапецию, есть средняя пропорциональная между параллельными сторонами трапеции.

11. Доказать, что отношение квадратов катетов равно отношению их проекций на гипотенузу.

12. 1) Построить два отрезка, квадраты которых относятся, как т : п.

2) Построить два отрезка, которые относились бы, как квадраты двух данных отрезков.

Теорема Пифагора.

13. Узнать, какими тремя последовательными целыми числами могут выражаться стороны прямоугольного треугольника.

14. Между двумя фабричными зданиями устроен покатый жёлоб для передачи материалов. Расстояние между зданиями равно 10 м, а концы жёлоба расположены на высоте 8 м и 4 м над землёй. Определить длину жёлоба.

15. 1) Точка внутри прямого угла удалена от его сторон на расстоянии а и b. Найти её расстояние от вершины.

2) Стороны прямоугольника равны 60 см  и  91 см. Чему равна его диагональ?

16. Требуется выфрезовать квадратную головку со стороной 32 мм. Чему должен быть равен наименьший диаметр круглого железа, годного для этой цели?

17. 1) Сторона квадрата равна а. Чему равна его диагональ?

2) Определить сторону квадрата, если она меньше диагонали на 2 см.

18. Диаметр бревна 12 см. Можно ли из этого бревна вытесать квадратный брус со стороной 10 см?

19. 1) Стороны прямоугольника равны а и b. Определить радиус описанного круга.

2) В круг вписан прямоугольник, стороны которого относятся, как 8:15. Определить эти стороны, если радиус круга равен 34 см.

20. 1) Катеты прямоугольного треугольника равны 8 дм и 18 см. Определить радиус описанного круга.

2) Катеты прямоугольного треугольника равны 16 см и 12 см. Определить медиану гипотенузы.

21. 1) В равнобедренном треугольнике боковая сторона равна 17 см, а основание 16 см. Определить высоту.

2) Определить стороны равнобедренного треугольника, если его высота равна 35 см, а основание относится к боковой стороне, как 48:25.

3) В равнобедренном треугольнике основание равно 4 см, а угол при нём равен 45 . Определить боковую сторону.

22. Стропильная ферма (черт. 7) имеет ноги АВ и СВ по 9 м и пролёт АС в 15 м. Определить высоту фермы BD.

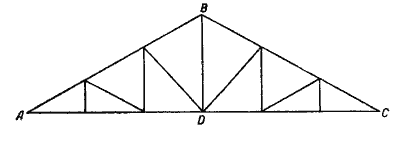
Черт 7.

23. 1) Биссектриса прямого угла делит гипотенузу прямоугольного треугольника на части, равные 2¹/₇ м   и  2 ⁶/₇ м. Определить катеты.

2) Катеты прямоугольного треугольника равны 15 см и 20 см. Из вершины прямого угла проведены высота и биссектриса. На какие отрезки разделилась гипотенуза?

24. 1) В равностороннем треугольнике определить высоту по данной стороне а.

2) В равностороннем треугольнике определить сторону по данной высоте h.

3) В равностороннем треугольнике высота меньше стороны на т. Определить сторону.

4) В прямоугольном треугольнике один из углов равен 30°, а больший катет равен 6 см. Определить две другие стороны этого треугольника.

25. 1) Боковые стороны треугольника равны: а = 25 см и b = 30 см, а высота h_с = 24 см. Определить основание с.

2) В треугольнике больший угол при основании равен 45°, а высота делит основание на части в 20 см и 21 см. Определить бoльшую боковую сторону.

3) Из одной точки проведены к данной прямой перпендикуляр и две наклонные. Определить длину перпендикуляра, если наклонные равны 41 cм и 50 см, а их проекции на данную прямую относятся, как 3:10.

26. 1) Диагонали ромба равны 24 см и 70 см. Определить сторону.

2) Определить диагонали ромба, если они относятся, как 3:4, а периметр равен 1 м.

27. 1) В равнобедренной трапеции основания равны 10 см и 24 см, боковая сторона 25 см. Определить высоту трапеции.

2) В равнобедренной трапеции боковая сторона равна 41 см, высота равна 4 дм и средняя линия 45 см. Определить основание.

28. Параллельно прямой дороге, на расстоянии 500 м от неё, расположена цепь стрелков; расстояние между крайними стрелками равно 120 м, дальность полёта пули равна 2,8 км. Какой участок дороги находится под обстрелом этой цепи?

29. На чертеже 8 изображена заклёпка ОСТ 302 (ОСТ —общесоюзный стандарт) с потайной головкой. Угол α  = 60°.

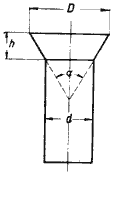
Черт. 8.

Вычислить:

1) D, если d = 16,5 мм и h = 7,5 мм;

2) d, если D = 30 мм и h = 9,5 мм;

3) h, если D = 35 мм и d = 22 мм.

Написать формулу, связывающую между собой D, d, h.

30. 1) В треугольнике ABC проведена высота AD.
Доказать, что AB²—AC² = BD² — CD²

2) Если М—некоторая точка высоты AD треугольника ABC,
то АВ² — AС² =  ВM² — СМ². Доказать.

31. 1) Доказать, что в прямоугольной трапеции разность квадратов диагоналей равна  разности  квадратов  оснований.

2) В прямоугольной трапеции меньшая диагональ равна наклонной боковой стороне. Определить бoльшую диагональ, если наклонная боковая сторона равна а, а меньшее основание равно b.

32. Из листа железа требуется выштамповать круглые шайбы, диаметром в 28 мм. Найти расстояние между прямыми, на которых следует расположить центры шайб (черт. 9).

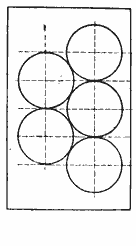
Черт. 9

33. 1) Радиус круга равен 89 дм, хорда 16 м. Определить её расстояние от центра.

2) О—центр; АСВ—хорда; OCD—радиус, перпендикулярный к ней, ОС=9 см и
CD = 32 см. Определить хорду.

3) Радиусы двух пересекающихся окружностей равны 13 см  и 15 см, а общая хорда равна 24 см. Определить расстояние между центрами.

4) АВ и CD—две параллельные хорды, расположенные по разные стороны от центра О окружности радиуса R= 15 см. Хорда АВ= 18 см, хорда CD = 24 см. Определить расстояние между хордами.

5) Две параллельные хорды АВ и CD расположены по одну сторону от центра О окружности радиуса R = 30 см. Хорда АВ = 48 см, хорда CD = 36 см. Определить расстояние между хордами.

34. Чтобы измерить диаметр большого шкива, установили штангенциркуль так, как показано на чертеже 10.

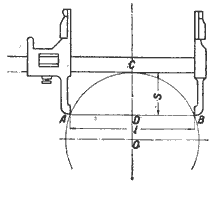
Черт. 10

Длина ножек штангенциркуля s = 25 мм, расстояние между концами ножек l =  200 мм.

1) определить длину диаметра D;

2) вывести формулу, выражающую зависимость D от s и l.

35. В сегменте хорда равна а, а высота h. Определить радиус круга.

36. Радиус круга равен 25 см; две параллельные хорды равны 14 см и 40 см. Определить расстояние между ними.

37. Расстояния от одного конца диаметра до концов параллельной ему хорды равны 13 см и 84 см. Определить радиус круга.

38. 1) К окружности радиуса, равного 36 см, проведена касательная из точки, удалённой от центра на 85 см. Определить длину касательной.

2) Из общей точки проведены к окружности две касательные. Радиус окружности равен 11 см, а сумма касательных равна 120 см. Определить расстояние от центра до исходной точки касательных.

3) К окружности радиуса, равного 7 см, проведены две касательные из одной точки, удалённой от центра на 25 см. Определить расстояние между точками касания.

39. Два круга радиусов R и r внешне касаются. Из центра одного круга проведена касательная к другому кругу, а из полученной точки касания проведена касательная к первому кругу. Определить длину последней касательной.

40. 1) Два круга касаются извне. Определить длину их общей внешней касательной (между точками касания), если радиусы равны 16 см и 25 см.

2) Радиусы двух кругов равны 27 см и 13 см, а расстояние между центрами равно
50 см. Определить длину их общих касательных.

41. Касательная и секущая, проведённые из общей точки к одной окружности, взаимно перпендикулярны. Касательная равна 12 м, а внутренняя часть секущей равна 10 м. Определить радиус окружности.

42. АВ и CD—параллельные прямые. АС—секущая, Е и F— точки пересечения прямых АВ и CD с биссектрисами углов С и А. Дано: AF = 96 см и СЕ =110 см. Требуется определить АС.

43. В тупоугольном равнобедренном треугольнике ABC основание АС =32 м, а боковая сторона 20 м. Из вершины В проведён перпендикуляр к боковой стороне до пересечения с основанием. На какие части он делит основание?

44. Катет АС= 15 см; катет СB = 8 см. Из центра С радиусом СВ описана дуга, отсекающая от гипотенузы часть BD, которую и требуется определить.

45. Дуга, описанная из вершины прямого угла прямоугольного треугольника радиусом, равным меньшему катету, делит гипотенузу на отрезки в 98 см и 527 см (начиная от меньшего катета). Определить катеты.

46. АВ—диаметр круга; ВС—касательная; D—точка пересечения прямой АС с окружностью. Дано: AD = 32 см и DC = 18 см. Требуется определить радиус.

47. АВ—диаметр; ВС и CD А — касательная и секущая. Определить отношение
CD : DA, если ВС равна радиусу.

Биссектриса в прямоугольном треугольнике.

48. В прямоугольном треугольнике биссектриса прямого угла делит гипотенузу в отношении 7:9. В каком отношении (считая части в том же порядке) делит её высота?

49. Определить катеты, если биссектриса прямого угла делит гипотенузу на части в
15 см и 20 см.

50. В равнобедренном прямоугольном треугольнике катет равен а. На какие части делит его биссектриса противолежащего угла?

51. В прямоугольном треугольнике биссектриса острого угла делит катет на отрезки
т и п (т > п). Определить другой катет и гипотенузу.

52. В прямоугольном треугольнике, катеты которого равны 15 дм и 2 м, проведены: высота из вершины прямого угла и биссектрисы обоих углов, образуемых высотой с катетами. Определить отрезок гипотенузы, заключённый между биссектрисами.

53. В прямоугольном треугольнике ABC катет ВС = 6 см и гипотенуза АВ =10 см. Проведены биссектрисы угла ABC и угла с ним смежного, пересекающие катет АС и его продолжение в точках D и Е. Определить длину DE.

54. В равнобедренном треугольнике ABC боковая сторона АВ = 10 м и основание
АС =12 м. Биссектрисы углов А и С пересекаются в точке D. Требуется определить BD.

55. 1) В равнобедренном треугольнике основание равно 30 см, а боковая сторона равна 39 см. Определить радиус вписанного круга.

2) В равнобедренном треугольнике центр вписанного круга делит высоту в отношении 17:15. Основание равно 60 см. Найти радиус этого круга.

Высота и стороны в прямоугольном треугольнике, ромбе и трапеции.

56. Из точки В проведены к данной прямой перпендикуляр ВС и наклонная ВА. На АС взята точка D, и прямая BD продолжена до пересечения в точке Е с прямой АЕ, перпендикулярной к АС. Определить АЕ, если ВА = 53 дм, AD = 8 дм и DC = 20 дм.

57. 1) В равнобедренном треугольнике основание равно 80 дм, а высота 20 дм. Определить высоту, опущенную на боковую сторону.

2) В равнобедренном треугольнике высота, опущенная на основание, равна 3 дм, а высота, опущенная на боковую сторону, равна 4 дм. Определить стороны этого треугольника.

3) Диагонали ромба равны 14 дм. и 48 дм. Определить его высоту.

58. 1) Гипотенуза АВ = 34 см; катет ВС =16см. Определить длину перпендикуляра, восставленного к гипотенузе из её середины до пересечения с катетом АС.

2) Радиус круга равен r. Определить длину хорды, проведённой из конца данного диаметра через середину перпендикулярного к нему радиуса.

59. В прямоугольном треугольнике ABC катет AС= 16 дм и катет BC=12 дм. Из центра В радиусом ВС описана окружность и к ней проведена касательная, параллельная гипотенузе (причём касательная и треугольник лежат по разные стороны гипотенузы). Катет ВС продолжен до пересечения с проведённой касательной. Определить, на сколько продолжен катет.

60. Из одной точки проведены к кругу две касательные. Длина касательной равна
156 дм, а расстояние между точками касания равно 120 дм. Определить радиус круга.

61. В прямоугольной трапеции основания равны 17 дм и 25 дм, а бoльшая боковая сторона равна 10 дм. Из середины этой стороны проведён перпендикуляр к ней до встречи с продолжением другой боковой стороны. Определить длину этого перпендикуляра.

Смешанные задачи на прямоугольный треугольник.

62. АС и СВ — катеты; CD — высота; DE || BC. Определить отношение АЕ : ЕС, если AС : СB = 4 : 5.

63. АС и СВ — катеты; CD — высота; DE_|_AC и DF_|_CB. Определить DE и DF,  если AС=75 дм и ВС=100 дм.

64. В двух равнобедренных треугольниках боковые стороны имеют одинаковую длину, а сумма углов при вершинах равна 180°. Основания относятся, как 9:40, а длина боковой стороны равна 41 дм. Определить основания.

65. 1) В треугольнике основание равно 60 м, высота 12 м и медиана основания  13 м. Определить боковые  стороны.

2) В прямоугольном треугольнике найти отношение катетов, если высота и медиана, выходящие из вершины прямого угла, относятся, как 40 : 41.

66. Определить радиус круга, описанного около равнобедренного треугольника, если основание и боковая сторона треугольника соответственно равны: 1) 6 дм и 5 дм;
2) 24 м и 13 м.

67. В прямоугольном треугольнике катеты равны 13 дм и 84 дм. Определить радиус вписанного круга.

68. Расстояние между центрами двух окружностей, лежащих одна вне другой, равно  65 дм; длина их общей внешней касательной (между точками касания) равна 63 дм, длина их общей внутренней касательной равна 25 дм. Опоедeлить радиус окружностей.

69. Длины двух параллельных хорд равны 40 дм и 48 дм, расстояние между ними равно 22 дм. Определить радиус круга.

70. В равнобедренной трапеции, описанной около круга, основания равны 36 см и 1 м. Определить радиус круга.

71. Около круга, радиус которого равен 12 см, описана равнобедренная трапеция с боковой стороной в 25 см. Определить основания этой трапеции.

72. Около круга радиуса r описана равнобедренная трапеция, у которой параллельные стороны относятся, как  т : n . Определить стороны этой трапеции.

73. АВ и АС—касательные к одному кругу с центром О, M—точка пересечения прямой АО с окружностью; DME — отрезок касательной, проведённой через М между АВ и АС. Определить длину DE, если радиус круга равен 15 дм, а расстояние AО=39 дм.

74. Катеты прямоугольного треугольника равны 15 дм и 20 дм. Определить расстояние от центра вписанного круга до высоты, проведённой на гипотенузу.

75. В прямоугольном треугольнике ABC из вершины С прямого угла опущен перпендикуляр на гипотенузу, и на нём, как на диаметре, описана окружность, которая на катетах СА и СВ даёт внутренние отрезки т и п. Определить катеты (т =12; n = 18).

76. В прямоугольном треугольнике катеты равны 75 дм и 100 дм. На отрезках гипотенузы, образуемых высотой, построены полукруги по одну сторону с данным треугольником. Определить отрезки катетов, заключённые внутри этих полукругов.

77. Если два  круга имеют внешнее касание, то их общая внешняя касательная есть средняя пропорциональная между их диаметрами. Доказать.

78. В трапеции ABCD меньшая диагональ BD перпендикулярна к основаниям AD и ВС; сумма острых углов А и С  равна 90°. Основание AD = a и ВС = b. Определить боковые стороны   АВ и CD.

ОТВЕТЫ
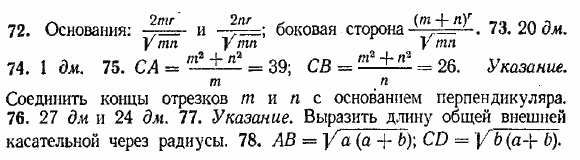